hihoCoder #1142 : 三分求极值-白红宇

#1142 : 三分·三分求极值

时间限制:

10000ms

单点时限:

1000ms

内存限制:

256MB

描述

这一次我们就简单一点了，题目在此：

在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y)，求点P到抛物线的最短距离d。

输入

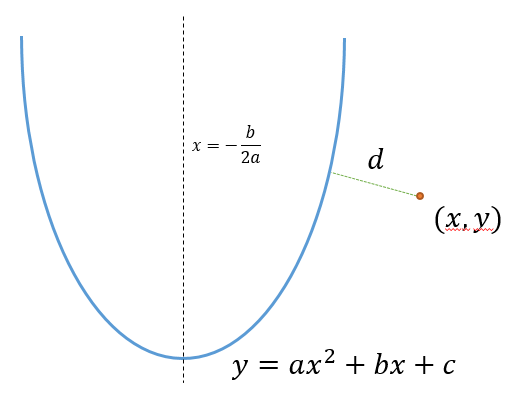
第1行：5个整数a,b,c,x,y。前三个数构成抛物线的参数，后两个数x,y表示P点坐标。-200≤a,b,c,x,y≤200

输出

第1行：1个实数d，保留3位小数(四舍五入)

样例输入

2 8 2 -2 6

样例输出

2.437

题目链接：https://hihocoder.com/problemset/problem/1142

【思路】

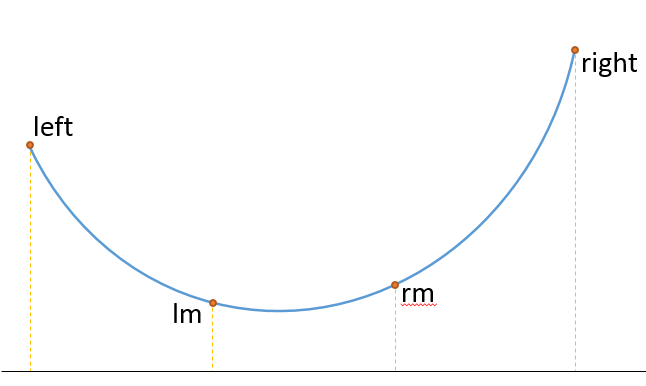
二分法作为分治中最常见的方法，适用于单调函数，逼近求解某点的值。但当函数是凸形函数时，二分法就无法适用，这时就需要用到三分法。

从三分法的名字中我们可以猜到，三分法是对于需要逼近的区间做三等分：

我们发现lm这个点比rm要低，那么我们要找的最小点一定在[left,rm]之间。如果最低点在[rm,right]之间，就会出现在rm左右都有比他低的点，这显然是不可能的。同理，当rm比lm低时，最低点一定在[lm,right]的区间内。利用这个性质，我们就可以在缩小区间的同时向目标点逼近，从而得到极值。

接下来我们回到题目上，抛物线和点之间的距离可以简单的用直线公式计算：即d = min{sqrt((X - x)^2+(aX^2+bX+c-y)^2)}该公式展开后为4次，需要采用求导等方法来求极值。对于计算机编程来说是很麻烦的一件事。
进一步观察题目，我们可以发现根据带入的X值不同，d的长度恰好满足凸形函数。而我们要求的最短距离d，正好就是这个凸形函数的极值。那么三分法不就正好可以用来解决这道题目了么？需要注意在解题过程中一定要想清楚如何划分区间，我们求的各个变量到底是什么含义。

下面给出AC代码：

1 #include 
      
        2 using namespace std; 3 double a,b,c; 4 const double eps=1e-4; 5 const double minn=-200; 6 const double maxn=200; 7 double x,y; 8 double solve(double X) 9 {10     return sqrt((X-x)*(X-x)+(a*X*X+b*X+c-y)*(a*X*X+b*X+c-y));11 }12 int main()13 {14   while(scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&x,&y)!=EOF)15   {16       double l=minn,r=maxn,midx,midy;17       while(r-l>eps)18       {19           midx=(l+l+r)/3;20           midy=(l+r+r)/3;21           if(solve(midx)<=solve(midy))22             r=midy;23           else l=midx;24       }25       printf("%.3lf\n",solve(l));26   }27   return 0;28 }